Читать книгу: «Решение задач по программированию на языке Форт (Forth). Версия 3»
Введение
С этой книгой вы изучите язык программирования Форт с нуля на конкретных примерах, минимум теории максимум практики. Почему Форт? Философия Форта – минимализм, простота, быстрота выполнения кода. Интерпретатор Форта компилирует все новые, определяемые слова, в словарь, немедленно после ввода, а это значит, что он сохраняет:
интерактивность REPL-среды и вы сразу видите результат своих действий и
быстроту компилятора
Потенциал Форта как языка программирования – безграничен. Хотя и являясь низкоуровневым, его можно превратить в язык высокого уровня и вводить любые типы данных и конструкции из других языков (Форт можно превратить в любой другой язык, диалект или создать свой).
Синтаксис этого ЯП (Языка Программирования) настолько прост, что его практически нет. Есть только одно главное правило – все Слова (именно так называются операторы языка и определяемые пользователем слова-функции) и числа должны быть разделены между собой хотя бы одним символом пробела и/или табуляции и/или переноса строки (то есть «любой символ пустоты, разделитель»).
Для кого эта книга?
Программировать на языке Форт настолько просто, что материал подойдет даже для детей. Не говоря уже об обучении, этому прекрасному виду человеческой деятельности, школьников, абитуриентов и студентов. Так что данным материалом может пользоваться любое заинтересованное лицо, независимо от возраста и рода человеческой деятельности. Сложность будет наращиваться постепенно, с нуля, с возможностью подтянуть сложные моменты и пропусков примитивов, уже подготовленными читателями.
Среда программирования SP-Forth – замечательно подойдет для наших целей. Программировать в этом консольном приложении можно начать сразу после быстрого скачивания и установки с официального сайта последней его версии. Он распространяется бесплатно. Работает он в режиме интерпретатора. Это значит, что после запуска системы программирования SP-Forth можно вводить команды или целую программу, после, нажав <Enter>, приложение обработает код и выдаст, предусмотренные результаты. Скачивание и установка SP-Forth не должен вызвать никаких сложностей, а потому этот процесс мы здесь опустим (в любом поисковике наберите «скачать SP-Forth», исполняемый файл запускается двойным кликом левой мыши по нему). После запуска Форта вы увидите:
Рис 1
Исторически сложилось, что основы программирования начинают изучать с первой программы, которая выводит на экран «Hello, World!», что по-русски означает «Здравствуй, Мир!».
Код для ЯП Форт будет следующий:
.( Hello world!)
или
S" Hello, World!" TYPE
После чего на экран будет выведено вышеупомянутое сообщение. Операторы ЯП (язык программирования) Форт <.(> и <S">: первый берет текст, следующий за ним до закрывающей кавычки – " (признак конца выводимой на экран строки) и печатает его на экран, второй создаёт строку адрес которой с ее длиной отправляется на стек. Затем оператор TYPE используя эти числа, адрес и его размер, как параметры также печатает сообщение. Главное «TYPE» должен идти сразу, во избежание ошибок при исполнении, это особенность работы системы. Обращайте внимание на пробелы – в форте они разделяют слова языка. Зачем нужен второй вариант, если первый проще и короче? Затем что он универсальный, так определяются в Форте строки, и они будут полезны в будущем.
Вот как должен выглядеть результат работы:

Рис 2
Третий вариант этой же программы будет выглядеть так:
: Hello_World ." Hello, World!" ;
Hello_World
Рис 3
Отличие в том, что определяется слово с именем приветствия, которое затем вызывается. Первые два варианта работают в режиме интерпретации, а последний – компиляции (в форт-словаре создается новое слово). Будучи универсальным, его можно вызывать многократно из различных мест программы или даже использовать это слово в своих библиотеках.
Так мы написали первую полноценную программку. Вместо «Hello_World», вы можете назвать «Start» или как захочется, главное придерживаться простого правила – названия должны быть информативными. Стиль программирования на ЯП Форт ничем не отличается от других языков, будет полезно в дальнейшем почитать об этом.
Так мы определили новое слово. Определение слова начинается с двоеточия, затем идет любой символ-разделитель (пробел, табуляция или перевода строки, но традиционно используется один пробел). После идёт имя слова, которое вы сами придумаете, далее код – реализация (последовательность операторов, чисел и других уже определённых слов), разделенных пробелами (и / или другими разделителями). Завершается точкой с запятой, также отделенный от кода пробелом.
Начало уже положено. Первая программа на Форте для начинающих выглядит довольно просто.
Добавим пару штрихов – комментарии:
Принято в каждом определении нового слова (на Форте) после названия писать стековый комментарий, обозначающий что слово берет со стека в качестве параметров и что оставляет на нем как результаты своей работы. Перепишем первое наше Форт-Слово:
: Hello_World ( -> ) ." Hello, World!" ; Hello_World
Так как Hello_World оставляет стек неизменным (не трогает его), то до и после стрелки пусто. Комментарий – это содержимое скобок.
Также существует второй способ комментирования кода до конца строки. Это символ – «\».
: Hello_World ( -> ) ." Hello, World!" ; Hello_World \ это программа, выводящая сообщение «Hello, World!»
Программирование без посторонней помощи не составит особой трудности даже, если вы только начинаете. В отличие от языков программирования С или С++, с которых также можно стартовать с нуля, все довольно наглядно и просто. На Форте можно практиковать программирование как онлайн, так и офлайн. Для первого варианта существует скрипт интерпретатор языка Форт на JavaScript (с его помощью можно создавать Форт программы прямо в браузере). Мы же будем ориентироваться на конкретный диалект Форта – SP-Forth. Он существует для всех популярных систем (Windows, Linux).
Обычно вторая задача при обучении программированию – это написание калькулятора. В Форте калькулятор писать не нужно, так как он поддерживает основные операции встроенными средствами, правда несколько в необычной форме, которая называется обратная польская запись или постфиксная. В математике вы привыкли писать формулы в инфиксной форме типа «(1 + 2) * 5 * (4 – 5)», где знак бинарной операции пишется между числами, например, в Лиспе сначала идёт операция, а затем операнд или операнды, а в Форте наоборот, сперва мы отправляем на стек операнды, затем операция выполняет действия над ними, оставляя результат там же. Стек это просто место в памяти, поддерживаемое на аппаратном уровне, следовательно, все операции над ними выполняются очень быстро, где будет хранится промежуточные данные. Так будет выглядеть работа с нашим калькулятором:
Операнд1 Операнд2 Операция. То есть вместо «1 + 2» на Форте мы должны написать «1 2 +».
1 2 +
Ok ( 3 ) \ 1+2=3 в скобках – это содержимое стека
1 2 *
Ok ( 3 2 ) \ 1*2=2 очередной результат на вершине стека
1 2 -
Ok ( 3 2 4294967295(-1) ) \ 1-2=-1 4294967295 – это без знаковый вариант числа -1
1 2 /
Ok ( 3 2 4294967295(-1) 0 ) \ 1/2=0 – это целочисленное деление, потому результат нуль
1 2 MOD
Ok ( 3 2 4294967295(-1) 0 1 ) \ остаток от деления 1/2
1 2 /MOD
Ok ( [7].. 4294967295(-1) 0 1 1 0 ) \ остаток от деления 1/2 и целая часть ½
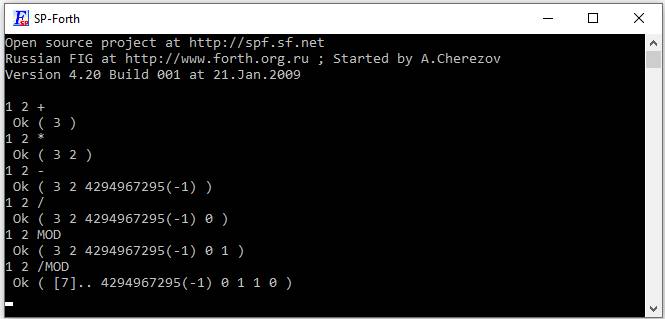
Рис 4
Вы можете сказать программирование на питоне – гораздо богаче, возможностями и будете правы. Но Форт быстрее и в качестве первого языка программирования гораздо проще и легче его освоить, а самое главное понятнее. Учить программирование на паскале, на мой взгляд уже не актуально. Хотя он и хорош для изучения различных алгоритмов, но это уже не современный язык программирования, со множеством избыточных конструкций и синтаксиса.
Приведем конкретные примеры на SP-Forth.
: ^2 ( A -> A^2 ) DUP * . ; \ возведение числа в квадрат
: ^3 ( A -> A^3 ) DUP DUP * * . ; \ возведение числа в куб
: ^4 ( A -> A^4 ) DUP * DUP * . ; \ возведение числа в четвертую степень
DUP – это слово которое просто дублирует число на вершине стека.
Возведём 5 в квадрат, для этого наберём на клавиатуре:
5 ^2
25 Ok
Получаем правильный ответ:
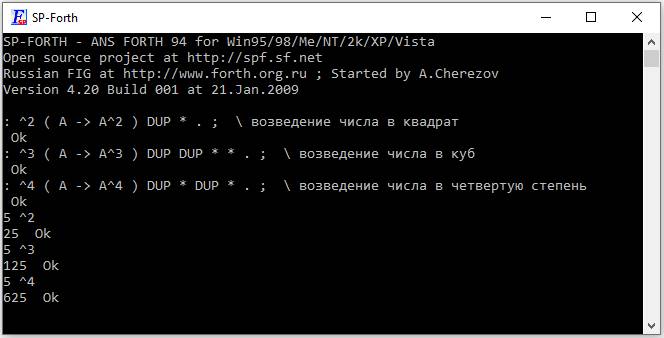
рис 5
Копировать код нужно аккуратно, при возведении в квадрат, получаем сообщение об ошибке. При «Копи пасте» куда-то делся символ табуляции между «;» и комментарием, вследствие видим «^ -2003 WORD OR FILE NOT FOUND», из-за нарушения синтаксиса. Наверное, это особенность системы. Почему-то «сглатывается» символ табуляции, а потому вставлен дополнительный символ пробела в коде выше, ниже приведен пример с ошибкой интерпретации:
: ^2 ( A -> A^2 ) DUP * . ; \ возведение числа в квадрат
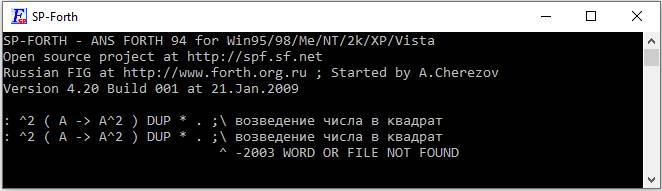
рис 6
Знаки табуляции нужны, чтобы структурировать логично, красиво и понятно код, например, в Python они элемент синтаксиса, без них ваш код не будет работать или как минимум будет выполняться некорректно, в Форте как и в других языках это элементы стиля программирования.
Также, вместо ^2, можно написать **2, в стиле python:
: **2 ( A -> A^2 ) DUP * . ; \ возведение числа в квадрат
5 **2
25 Ok
В итоге получаем тот же ответ, но оформление, стиль изменились. Не забывайте «**2» – это слово, а значит он отделяется пробелом от операнда «5» (до и после, если за ним будут другие инструкции). Это одно из самых главных отличий Форта от других языков.
Для начала этого достаточно. Далее при решении конкретных задач, процесс станет более понятным и осознанным. Приступим.
BEGIN 1-10
Практиковаться программированию на Форте будем с задач из книги М. Э. Абрамян "1000 задач по программированию Часть I Скалярные типы данных, управляющие операторы, процедуры и функции" 2004. Автор пишет, что получить задачник можно по e-mail: mabr@math.rsu.ru или за подробностями обращайтесь к веб ресурсу ptaskbook.com. Текст задач я приводить не буду, дабы исключить плагиат. Думаю, пояснения к коду с описанием слов (функций-программ) должно быть достаточно, в противном случае обращайтесь к первоисточнику за текстом задач.
Пример 1. Итак, начнем, (для простоты вначале мы будем рассматривать все входные параметры как целые числа, далее мы перепишем код для вещественных аргументов, где об этом указано в условии задачи). Вот и решение первой задачи:
: B1 ( A -> P ) 4 * ; \ P=4*A
B – это сокращение от BEGIN, что обозначает первую группу заданий (мы и далее будем использовать такой вид названий в последующих группах заданий), затем слитно пишется номер примера, как часть названия слова. Сразу после имени в скобках пишется комментарий стековой нотации. Так принято в Форте. В данном случае Слово-функция B1 берет один параметр A (четырехбайтовое целое число и оставляет другое того же типа). A – сторона квадрата – вход функции, P – его периметр – возвращаемое функцией значение. Тело – очень короткое, просто умножает число на вершине стека на 4 (не забываем, что в Форте обратная польская запись, сначала идут операнды, затем операция).
Теперь чтобы пользоваться нашим словом, например, чтобы посчитать периметр квадрата со стороной 3, наберем следующий код:
3 B1 .
12 Ok

Рис 7
Точка «.» – это стандартное форт слово, которое печатает число на вершине стека на экран.
Напомним, общий вид определения нового слова в Форте:
: Название-Слова ( стек до выполнение –> после ) Код-Тела-Функции ; \ комментарий
Пример 2. Посчитаем площадь квадрата:
: B2 ( A -> S ) DUP * ; \ S=A^2
Мы просто дублируем число на вершине стека (для чего используем оператор языка Форт – DUP, от английского слова дублировать) и умножаем его на себя. Данный пример можно оформить более красиво для использования в ваших будущих программах и включать как библиотеку или как расширение стандартного словаря с последующим сохранением как новой версии Форта.
: SQR ( A -> A^2 ) DUP * ; \ A^2 – вычисление квадрата числа, или
: ^2 ( A -> A^2 ) DUP * ; \ или
: **2 ( A -> A^2 ) DUP * ; \ отличие только в названии
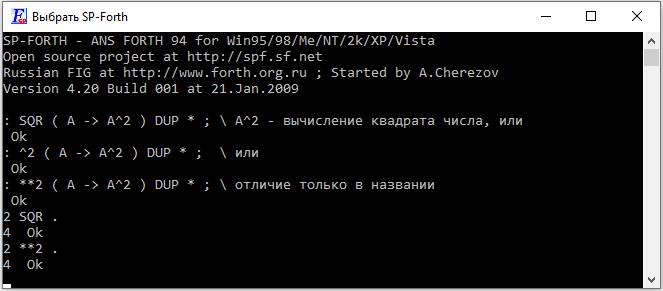
Рис 8
Результат тот же, так как слова делают одно и тоже. Имя слову можно давать любое – area, square (не только заглавными буквами, так просто исторически сложилось на Форте, что все операторы языка пишутся не строчными буквами), в зависимости от контекста. Какой вариант нравится, тот и можете использовать. Или все сразу, так тоже можно.
Пример 3. По сторонам прямоугольника нужно вычислить его Площадь и Периметр:
: B3 ( A B -> S P ) \ ( S=A*B P=2*(A+B) )
2DUP ( A B -> A B A B ) \ Слово 2DUP, дублирует сразу два числа
* ( A B A B -> A B A*B=S ) \ Площадь вычислен – это просто произведение сторон
ROT ROT ( A*B=S A B ) \ оператор ROT вытаскивает 3-ий от вершины параметр на вершину
\ применив его два раза на вершине мы получаем A B и вычисленный под ним Площадь
+ 2* ; \ складываем A и B, и умножив на 2, оператором 2*, получаем периметр
Слово «2*» делает тоже самое что и два слова «2 *», только короче и проще, и главное одно слово выполняется быстрее, чем два.
В итоге на стеке мы получаем Площадь и Периметр. Чтобы напечатать результаты на экран из примеров нужно просто ввести точку с клавиатуры «.» и затем нажать «Enter». Сначала напечатается вершина, т. е. периметр, в данном примере, затем повторив действия площадь. Чтобы изменить порядок печати, наберите слово SWAP, который меняет местами 2 числа на вершине стека ( A B -> B A), т.е., например чтобы напечатать площадь и периметр прямоугольника со сторонами 1 и 2 введём следующее:
1 2 B3 SWAP . .
2 6 Ok
Площадь равна «1*2=2», а периметр равен «2*(1+2) = 6». Слово работает корректно и вычисляются площадь и периметр соответственно стековой нотации, а выводятся по условию задачи.
Перепишем слово «B3» более красиво:
: B3 ( A B -> S P ) \ ( S=A*B P=2*(A+B) )
2DUP \ A B -> A B A B
* \ A B A B -> A B A*B=S
ROT ROT \ A B S -> S A B
+ 2* \ S A B -> S (A+B)*2=P
;
Удалены лишние комментарии, оставлена только стековая нотация.
Слово «B3» считает площадь и периметр и ничего не выводит на экран. Его можно использовать, как и первый вариант, результат будет тот же:
1 2 B3 SWAP . .
Проверьте этот факт самостоятельно.

рис 9
Последний вариант выглядит более профессионально, первый (с максимальным количеством комментариев) только для учебных целей, чтобы освоится с новыми словами языка.
Пример 4. Нужно вычислить длину круга зная его диаметр:
: B4 ( D -> L ) 314 * ; \ L=Pi*D*100
Ответ буде в 100 раз больше для целочисленных данных («Пи» вместо 3,14 взяли 314), таким образом избавились от дробной части. Так себе решение. Напишем слово:
: .2 ( A -> {[A/100],[A%100]} )
100 /MOD . 8 EMIT 44 EMIT .
;
Слово «.2» печатает результат, который в 100 раз больше, как два разных числа «склеенных» вместе (целая часть от «A/100» и его дробная часть – 2 знака десятичной дроби) с запятой. Теперь вычислим длину окружности диаметром 1 – результат точный для «Пи»=3,14:
1 B4 .2
3,14 Ok

Рис 10
Подробно рассматривать код слова «.2» не будем, а перепишем так, чтобы можно было работать с вещественными числами. Для этого в SP-Forth нужно подключить соответствующие библиотеки. Скопируйте и вставьте следующие две строчки:
S" lib\include\float.f" INCLUDED
S" lib\include\float2.f" INCLUDED
Можно только вторую строчку (вызов второй, после первой выводит много сообщений типа «isn't unique (lib\include\float2.f)» – это не ошибки, означает, что слова с таким именем ранее были введены в систему).
Теперь чтобы ввести вещественное число, скажем 0,5, нужно набрать на клавиатуре следующее:
5E-1 или 5e-1
До E – это мантисса (число), после экспонента (степень). Мантисса и экспонента могут быть как положительными (знак не требуется), так и отрицательными (в данном случае степень -1, что значит 10 в минус первой степени).
После ввода, вещественное число размещается на соответствующем ей вещественном стеке. Поэтому мы не видим его после вывода слова Ok в скобках, так как это другой стек для целых чисел. Чтобы его увидеть нужно ввести «F.». Итак, чтобы проверить, что всё работает как надо, введём код:
5E-1 F.
В ответ увидим:
0.5000000 Ok
Слово «F.», аналогично, как и «.» выводит число на экран, только не с целочисленного стека, а с вещественного.
Теперь мы можем переписать пример 4 для вещественных аргументов:
: B4 ( D -> L ) \ L=Pi*D
314E-2 F* ;
Вместо 314E-2 можно набрать 3.14E, результат тот же. Посчитаем длину окружности диаметром 0,5, набрав следующее:
5E-1 B4 F. \ вызываем слово, которое считает длину окружности и «F.» печатает его результат
1.5700000 Ok
Мы готовы переписать таким же образом код первых трех примеров для случая с вещественными аргументами, сделав их более универсальными.
Пример 1:
: B1 ( A -> P ) 4E F* ; \ P=4*A
Знак «*» заменяется на «F*», четверка вводится как вещественное число (операция «F*», в отличие от «*» производит операцию над вещественными числами на вещественном стеке). Теперь проверим, посчитаем периметр квадрата со стороной 0,5:
5E-1 B1 F.
2.0000000 Ok
Ответ 2 (0,5*4=2) что является правдой.
Данный пример, так же можно преобразовать, написав в стиле:
: B1 ( A -> P ) \ P=4*A
4E F*
;
Но он настолько маленький и примитивный, что едва ли это необходимо, проще и лаконичней всё оставить в одной строчке. В более сложных и больших примерах код нужно писать структурированным, понятным и разумеется в едином стиле.
Пример 2:
: B2 ( A -> S ) FDUP F* ; \ S=A^2
Опять DUP превращается в FDUP, умножение как в первом случае. Проверим работу слова. Посчитаем площадь квадрата со стороной 0,5:
5E-1 B2 F.
0.2500000 Ok \ 0,5*0,5 = 0,25
Иллюстрация примеров 1,2 и 4 для вещественных аргументов:
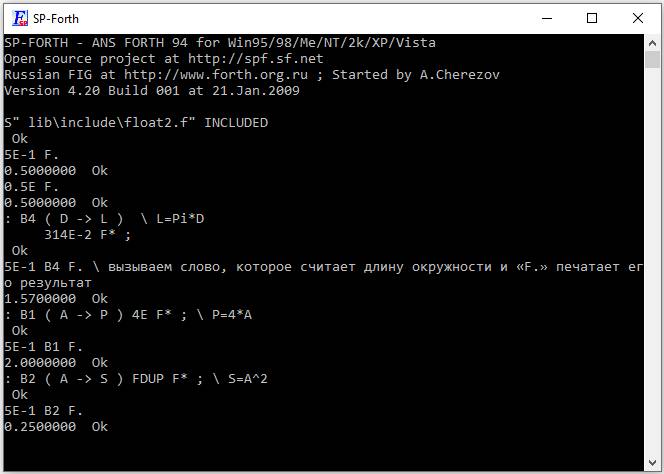
рис 11
Пример 3: Расчет площади и периметра прямоугольника.
: B3 ( A B -> S P ) \ ( S=A*B P=2*(A+B) )
FOVER FOVER \ A B -> A B A B
F* \ A B A B -> A B A*B=S
FROT FROT \ A B S -> S A B
F+ 2E F* \ S A B -> S (A+B)*2=P
;
Первая строка стандартное, уже знакомое начало слова на Форте. Далее:
Вторая строка «FOVER FOVER ( A B -> A B A B )». Слова 2FDUP – нет в словаре, «FOVER» копирует элемент под вершиной вещественного стека на вершину, двойное повторение аналогично целочисленному «2DUP».
Третья – умножение двух чисел на вершине вещественного стека. Получаем площадь прямоугольника.
Четвертая, как и для целочисленного варианта слова (ROT заменяется на FROT).
Пятая сложение двух чисел на вершине вещественного стека и удвоение результата.
Шестая завершение слова, в итоге на вершине стека получаем 2 числа – площадь и периметр.
Проверим работу слова B3 на сторонах прямоугольника 0,2 и 0,3:
2E-1 3E-1 B3 FSWAP F. F.
0.0600000 1.0000000 Ok
Как можете увидеть ниже всё работает верно:
S = 0,2*0,3=0,06
P=2*(0,2+0,3)=2*0,5=1
0,2 и 0,3 можно вводить и в следующем виде: 0.2E и 0.3E. Самостоятельно можете убедиться, что слово «F.» выведет на экран тоже самое значение.
Код «2E-1 3E-1 B3 FSWAP F. F.» можно собрать в отдельное слово, если не приятно работать с таким количеством команд:
: B3. ( S P -> S. P. ) B3 FSWAP F. F. ;
Ok
2E-1 3E-1 B3.
0.0600000 1.0000000 Ok
Согласно логике Форта «B3.» аналогично «.» означает печать результатов слова «B3».
Вы можете спросить зачем такие сложности? Код становится универсальным, мы отделяем вычисляемую часть от метода вывода данных на экран, его можно использовать при определении других слов, включать в свои библиотеки, и использовать в других задачах как отдельную функцию.
Вы можете заметить, что, в примере 3, каждая строка кода сопровождается комментарием, которая поясняет изменения на стеке. Так как все операции и манипуляции, в данном примере, производятся только с вещественным стеком, мы это никак не обозначаем, когда слово будет работать с обоими стеками сразу, вещественный стек будем выделять так: «F: A B A*B=S -> S A B», изменения целочисленного стека дополнительно выделять не будем. Существует еще и стек возвратов. Будьте осторожны, любые неосторожные манипуляции приведут к некорректным результатам, в лучшем случае, в худшем вызовут сообщения об ошибке.
Так же обратите внимание, что комментарии выравниваются так чтобы они выстроились в вертикальную линию, даже те строчки, в которых нет кода, исключительно для удобства чтения (транслятор Форта «проглотил» знаки табуляции, поэтому между кодом и комментарием остался 1 пробел).
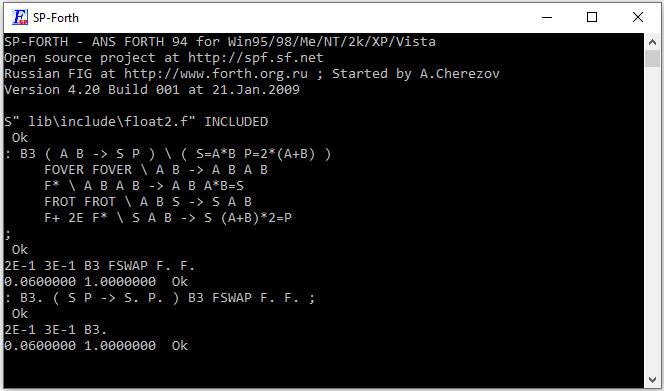
рис 12
Пример 5. Здесь вычисляется объем куба и площадь его боковой поверхности. Вначале приведем работу с целочисленным аргументом.
: B5 ( A -> V=A^3 S=6*A^2 )
DUP 2DUP \ A -> A A A A
* * \ A A A A -> A A^3
SWAP \ A A^3 -> A^3 A
DUP * 6 * \ A^3 A -> A^3 A^2*6 – V=A^3 S=6*A^2
;
Поясним код:
Во второй строчке кода 2DUP, в отличие от DUP дублирует сразу 2 верхних элемента, совместное использование (DUP и 2DUP) оставляют четыре числа A.
В третьей, два умножения «* *» приводят к вычислению куба ( A A A A -> A A*A*A=A^3 ).
В четвертой, SWAP меняет куб числа «A» с ним самим местами ( A A^3 -> A^3 A ).
В пятой, «DUP *» (A^3 A -> A^3 A*A ), возводит в квадрат число на вершине стека, а «6 *» умножает его на шесть. В результате получаем площадь боковой поверхности.
Вызовем написанное слово с параметром 15 (сторона куба):
15 B5
Ok ( 3375 1350 )
3375=15*15*15 и 1350=6*15*15, все верно, слово работает корректно.
То же самое с вещественными числами:
: B5 ( A -> V S ) \ V=A^3 S=6*A^2
FDUP FDUP FDUP \ A -> A A A A – 2FDUP SP-Forth не понимает
F* F* \ A A A A -> A A*A*A=A^3
FSWAP \ A A^3 -> A^3 A
FDUP F* \ A^3 A -> A^3 A*A
6E F* \ A^3 A*A -> A^3 6*A^2
;
Проверим написанный код, возьмем куб со стороной 1,5:
15E-1 B5 F. F.
13.500000 3.3750000 Ok \ 6*1.5^2 = 13.5 1.5^3 = 3.375
Помните, что оператор «F.» печатает то, что лежит на вершине стека. Если вам нужен другой порядок можно применить FSWAP, так при необходимости вывести сперва объем, как в стековой нотации, можно набрать следующее:
15E-1 B5 FSWAP F. F.
3.3750000 13.500000 Ok
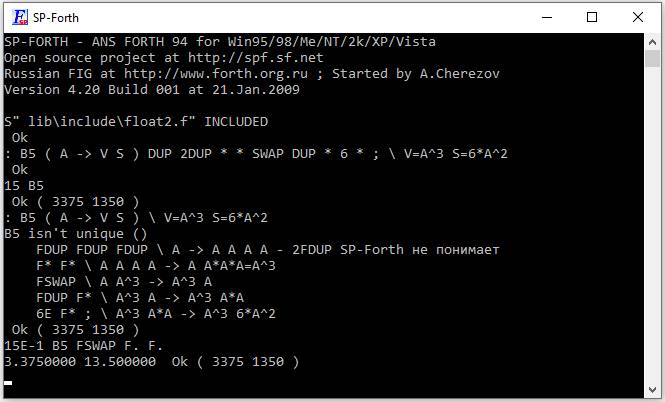
рис 13
Самостоятельно напишите слово «B5.» для вещественного варианта и корректный вывод результатов с целочисленного стека в первом случае.
Пример 6. Здесь необходимо вычислить объем и площадь поверхности прямоугольного параллелепипеда, через его ребра.
: B6 ( A B C -> S V ) \ S=2*(A*B+B*C+A*C) V=A*B*C )
DUP 2OVER \ A B C -> A B C C A B
DUP 2OVER \ A B C C A B -> A B C C A B B C A
ROT * \ A B C C A B B C A -> A B C C A B C A*B
ROT ROT * + \ A B C C A B C A*B -> A B C C A (A*B+B*C)
ROT ROT * + \ A B C C A A*B+B*C -> A B C (A*B+B*C+C*A)
2* \ A B C (A*B+B*C+C*A) -> A B C (A*B+B*C+C*A)*2
SWAP 2SWAP \ A B C (A*B+B*C+C*A)*2 -> (A*B+B*C+C*A)*2 C A B
* * ; \ (A*B+B*C+C*A)*2 (C*A*B)
Где (A*B+B*C+C*A)*2 – это площадь поверхности, а (C*A*B) – объем.
В данном примере появляется 3 параметра, что не слишком усложняет задачу, и по-прежнему мы не будем использовать переменные в явном виде, манипулируя только с данными на стеке.
В коде для вещественных чисел надо, чтобы число элементов не превышало максимума, из-за его ограниченности произойдет ошибка. Проверим сколько вмещает наша система, для этого наберем следующие команды:
FDEPTH \ Это слово возвращает количество элементов в вещественном стеке
Ok ( 0 ) \ 0 элементов
5E-1 FDEPTH \ введем 1-ое число
Ok ( 0 1 ) \ 1 элемент на вещественном стеке
5E-1 FDEPTH \ введем 2-ое число
Ok ( 0 1 2 ) \ 2 элемента
5E-1 FDEPTH \ введем 3-е число
Ok ( 0 1 2 3 ) \ 3
5E-1 FDEPTH \ введем 4-ое число
Ok ( 0 1 2 3 4 ) \ 4
5E-1 FDEPTH \ введем 5-ое число
Ok ( [6].. 1 2 3 4 5 )
5E-1 FDEPTH \ введем 6-ое число
Ok ( [7].. 2 3 4 5 6 )
5E-1 FDEPTH \ введем 7-ое число
Ok ( [8].. 3 4 5 6 7 )
5E-1 FDEPTH \ ошибка !!!
Если после ошибки ввести «F.» получим:
infinity Ok
После ошибки лучше перезапустить SP-Forth. Так же не забывайте о подключении библиотек заново для работы с вещественными числами. Существует слово DEPTH для обычного стека, которое также оставляет количество его элементов, не считая возвращаемый параметр, но для целочисленного стека.

рис 14
Или можете набрать «FINIT» для переинициализации.

рис 15
Перепишем Пример 6 для вещественных чисел.
: B6 ( A B C -> S V ) \ S=2*(A*B+B*C+A*C) V=A*B*C )
FOVER FOVER F+ \ A B C -> A B C (B+C)
FROT FROT F* \ A B C (B+C) -> A (B+C) B*C
FROT \ A (B+C) B*C -> (B+C) B*C A
FOVER FOVER F* \ (B+C) B*C A -> (B+C) B*C A B*C*A
F. \ 1-ый результат – объем
FROT F* F+ 2.E F* \ (B+C) B*C A -> {B*C+A*(B+C)}*2
F. \ 2-ой результат S=2*(A*B+B*C+A*C)
;
Теперь можно проверить как работает написанное слово:
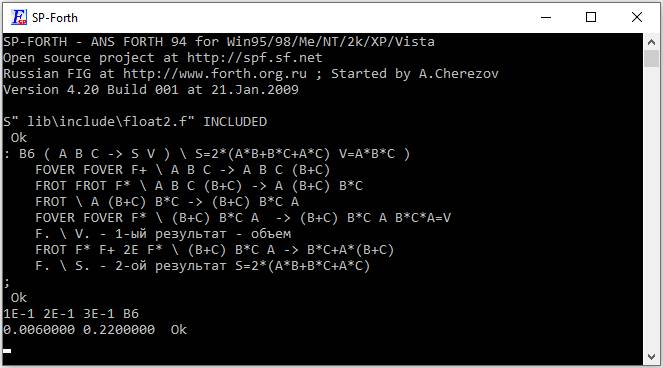
рис 16
1E-1 2E-1 3E-1 B6
0.0060000 0.2200000 Ok
Объем прямоугольного параллелепипеда 0,006=0,1*0,2*0,3 и площадь его поверхности 0,22=2*(0,1*0,2+0,2*0,3+0,1*0,3).
Проведите тесты с целочисленным вариантом. Как вывести результаты, нужны ли дополнительные манипуляции со стеком? Последний вариант получился не универсальным, печать результатов в самом слове. Можете это исправить как уже было сделано ранее?
Пример 7. Зная радиус окружности, посчитаем его длину и площадь.
: B7 ( R -> L S) \ L=2*Pi*R и S=Pi*R^2
DUP 2* 314 * \ R -> R R*2*314=L
SWAP \ R L -> L R
DUP 314 * * \ L R -> L R*R*314=S
;
Целочисленный вариант принимает целое значение радиуса и выдает результат в 100 раз больше. Надеюсь по комментариям стековой нотации работа слова понятна (она довольно тривиальна).
Результаты теста с ранее написанным словом «.2»:
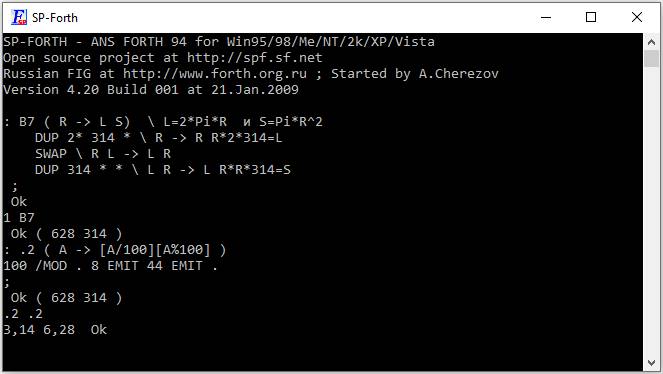
рис 17
Для печати с тем же порядком как в стековой нотации наберите «1 B7 SWAP .2 .2»
Код для вещественного аргумента:
: B7 ( R -> L S) \ L=2*Pi*R и S=Pi*R^2
FDUP 2E F* 314E-2 F* \ R -> R 2*Pi*R=L
FSWAP \ R L -> L R
FDUP 314E-2 F* F* \ L R -> L R*R*3.14=S
;
Вычислим длину окружности и площадь круга радиусом 0,1:
1E-1 B7 F. F.
0.0314000 0.6280000 Ok
0.0314000=0,1*0,1*3,14 и 0.6280000= 2*3,14*0,1. Результаты теста корректны.

рис 18
Пример 8. Простая задачка на вычисление среднего арифметического двух целых чисел:
: B8 ( A B -> [A+B]/2 ) + 2/ ;
1 3 B8
Ok ( 2 )
Мини-код работает правильно (1+3)/2=2. Ниже приведем код для вещественного аргумента:
: B8 ( A B -> [A+B]/2 ) F+ 2E F/ ;
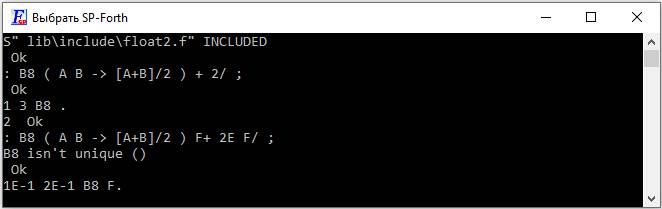
рис 19
1E-1 2E-1 B8 F.
0.1500000 Ok
0.15 = (0.1+0.2)/2 – ИСТИНА
Пример 9. Среднее геометрическое двух чисел – это квадратный корень из их произведения. Сразу напишем код для вещественного аргумента, так как возможности извлечение корня для целых чисел в системе SP-Forth нет, для этого придётся переводить целое число в вещественное извлечь квадратный корень, затем перевести обратно в целый вид, поэтому здесь такие хлопоты не оправданы, но если где-то вам это понадобится, то такое возможно.
: B9 ( A B -> SQRT[A*B] ) F* FSQRT ;
Очень короткий и понятный код, который тестируем ниже:
3E-1 75E-1 B9 F.
1.5000000 Ok \ 1,5 = Корень_Квадратный_из(0,3*7,5) – ИСТИНА

рис 20
Этот и предыдущий примеры можно оформить красиво, для дальнейшего использования в математических вычислениях или в других программах, как ваши библиотечные функции.
: MIDDLE_ARITHMETIC ( A B -> [A+B]/2 ) F+ 2E F/ ;
: MIDDLE_GEOMETRIC ( A B -> SQRT[A*B] ) F* FSQRT ;
За грамотные английские названия не ручаюсь.
Пример 10. Вход два числа, не равные нулю. Вычислим сумму, разность, произведение и частное их квадратов, те есть:
: B10 ( A B -> A^2+B^2 A^2-B^2 A^2*B^2 A^2/B^2 )
SWAP DUP * SWAP DUP * \ A B ->A^2 B^2
2DUP + \ A^2 B^2 -> A^2 B^2 (A^2+B^2)=(+)
ROT ROT 2DUP – \ A^2 B^2 (+) -> (+) A^2 B^2 (A^2-B^2)=(-)
ROT ROT 2DUP * \ (+) A^2 B^2 (-) -> (+) (-) A^2 B^2 (A^2*B^2)=(*)
ROT ROT / \ (+) (-) A^2 B^2 (*) -> (+) (-) (*) (A^2/B^2 )=(/)
;
Протестируем на числах 4 и 2.
4 2 B10
Ok ( 20 12 64 4 )
Всё корректно, проверяйте самостоятельно. В комментариях я сократил сумму, разность и произведение квадратов до соответствующих операций в скобках. Специально подобраны такие числа, чтобы результат деления был целочисленным, но это не обязательно – код для вещественных аргументов избавит нас от таких неудобств:
: B10 ( A B -> A^2+B^2 A^2-B^2 A^2*B^2 A^2/B^2 )
FSWAP FDUP F* \ A B -> B A^2
FSWAP FDUP F* \ B A^2 -> A^2 B^2
FOVER FOVER F+ \ A^2 B^2 -> A^2 B^2 (A^2+B^2)=(+)
FROT FROT FOVER FOVER F- \ A^2 B^2 (+) -> (+) A^2 B^2 (A^2-B^2)=(-)
FROT FROT FOVER FOVER F* \ (+) A^2 B^2 (-) -> (+) (-) A^2 B^2 (A^2*B^2)=(*)
FROT FROT F/ \ (+) (-) A^2 B^2 (*) -> (+) (-) (*) (A^2/B^2)=(/)
;
Тест примера 10:
1E-1 2E-1 B10 F. F. F. F.
0.2500000 0.0004000 -0.0300000 0.0500000 Ok
Не забываем, что оператор F. Печатает число с вершины стека, поэтому сначала печатается частное, затем произведение, после чего разность и в конце сумма.
0,25 = 0,01/0,04; 0,0004 = 0,01*0,04; -0,03 = 0,01-0,04; 0,05 = 0,01+0,04.
Если вам нужен другой порядок вывода результатов, то самостоятельно решите эту задачу для обоих вариантов, слова ниписаны в соответствии со стековой нотацией.
Полезные слова (если переименовать и разбить некоторые из приведенных выше, то получим список, который можете использовать как свою маленькую математическую библиотеку):
: SquarePerimeter ( a -> P=4*a ) 4E F* ;
: SquareArea ( a -> S=a*a ) FDUP F* ;
: RectanglePerimeter ( a b -> P=2*[a+b] ) F+ 2E F* ;
: RectangleArea ( a b -> S=a*b ) F* ;
: CircleLength ( r -> l=2*Pi*r ) 2E FPI F* F* ;
: CircleArea ( r -> S=Pi*r*r ) FDUP F* FPI F* ;
: CubeVolume ( a -> V=a*a*a ) FDUP FDUP F* F* ;
: CubeLateralSurfaceArea ( a -> S=6*a*a ) FDUP F* 6E F* ;
: RectangularPrismVolume ( a b c -> V=a*b*c ) F* F* ;
: RectangularPrismLateralSurfaceArea ( a b c -> S=2*[a*b+b*c+a*c] ) FOVER FOVER F+ FROT FROT F* FSWAP FROT F* F+ 2E F* ;
: ArithmeticMean ( a b -> [A+B]/2 ) F+ 2E F/ ;
: GeometricMean ( a b -> SQRT[A*B] ) F* FSQRT ;
Тесты проведите самостоятельно.
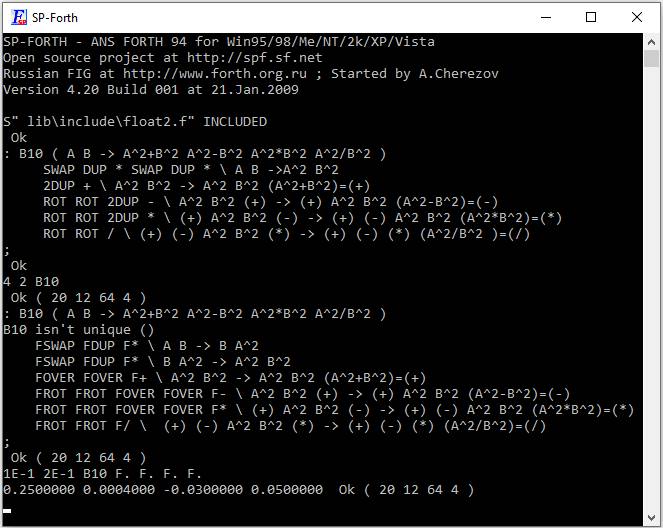
рис 21 Результат работы целочисленного и вещественного вариантов примера B10
Начислим
+10
Покупайте книги и получайте бонусы в Литрес, Читай-городе и Буквоеде.
Участвовать в бонусной программе
